Training models on their own outputs

Lets start by considering the question: what is the relationship between model inputs and model outputs?

We can imagine three categories settings might fit into:

- General setting: Model outputs are used as later model inputs. More generally, there's some map from model outputs to model inputs. For example, model actions -> next world state (in RL, the next Go board position, etc.), model output distribution -> generated text, etc.  

- Fixed input set: While the set of inputs are fixed ahead of time, the model can influence which inputs are chosen. Call the thing that decides inputs based on model outputs the environment. Active learning, and auto-induced distributional shift seem to fall into this category. 

- Input order unaffected by model outputs: (input, model output) pairs are used as targets for training, but model outputs don't lead to different inputs, and the input distribution is fixed and unaffected by the model. This is a standard learning setting. Because the behavior of the model cannot change the data, causality goes one way, and this is uninteresting.

Note that Fixed input set has two key variables: how large the input set is, and how complex the environment is. For the environment, there are a few parameter choices. Does it know about:

- Past inputs (and which ones?)

- Past model outputs (and which ones?)

We can also try and bound the environment in various ways. Maybe it is only allowed to run in time O(MaxRuntime(modelSize)), for some function MaxRuntime. Or maybe it has to pre-define all model inputs ahead of time. There are many other kinds of choices here studied in the online learning literature, for various choices of "adversaries" (environment=adversary).

Note that if the input set is large enough (to say, include model outputs) and the environment is expressive enough, Fixed input set includes the General Setting

"Simplest setting": Fixed model

It seems kind of weird to talk about online learning when the model isn't changing, so we will focus on the General Setting.

Lets say that we have some transition function

newX = T(x, model(x)) that outputs the next input, given current input and the output of the model on that input. Since our model is fixed, we can make a new model F(x) = T(x, model(x)). Then we are just studying iterated function application, where F specifies the transition dynamics. 

Iterated function application is a really rich field of study. This is partly because the framework could specify anything, such as training a model on x and outputting a new dataset y based on that trained model. x could also encode a model as part of the state, and then we're doing fine tuning. Constraining the model to be a neural network helps a little, since once we fix the size of the model it constrains the runtime of F and thus limits the functions it can compute. But we are still effectively dealing with a (continuous) circuit of some fixed depth and width, and that's a very large class of functions. And if we are using an RNN with a flexible number of steps, it's computationally universal, and we don't have much hope of analysis.

Other relevant perspectives here are Deep Equilibrium Models, Denoising models, and research around using more compute at test time.

Can we characterize when iterated functions are open-ended?

Essentially, that would be when they don't have an equilibrium point. We can look at some constructive examples. Fractals seem to have open-ended complexity, see the mandelbrot zooms that keep having interesting new patterns.

Alternatively, we can represent any model of computation as a state and transition function. This gives a nice mapping from transition functions to complexity classes. Now, by talking about which complexity class our transition function is in, we can ask about the difficulty of questions about predicting it's behavior.

I think that this is a useful perspective I want to investigate more from the lens of "what models of computation+algorithms are open-ended", but you need to make quite a few assumptions before anything is tractable.

Updating Model

While the fixed model setting ended up being fairly complex, that was mostly the result of overgeneralizing. 

As mentioned above, one way to think about this is online learning (or more generally, partial monitoring). There's a lot of detailed literature on that topic. It's a useful perspective, and looking at causality is important as feedback loops can cause all kinds of problems. 

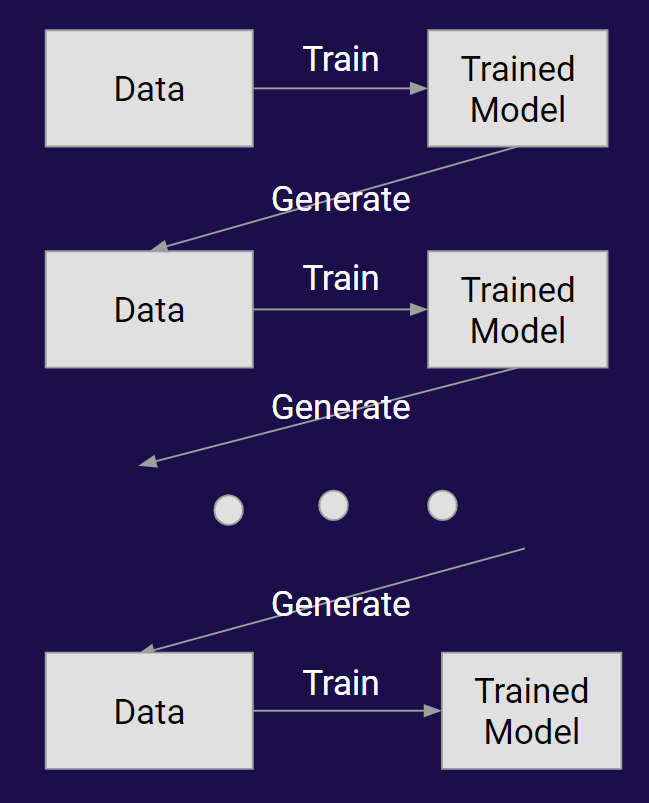
However, we can also consider something a little simpler: what if we just take the model outputs, and feed them back in as inputs? What happens?

Some concrete ways we could do this:

- Generative models that output data sampled from some distribution. That data is then used to either train a new generative model:

or to update the model:

- A similar process, but for classification, with data pulled from some external distribution

Classifiers

Starting with a linear binary classifier, I can do some detailed experiments and analysis. Here's how the setup works:

1. The classifier will be "dot product with a vector, the label is the sign" (linear classifier with no offset)

2. Generate data points sampled from Normal(0, 1) in D dimensions.

3. Generate a random vector as our "ground truth". Make N labeled points, and use this to train a classifier.

4. Use that classifier to produce more data.

5. Train a new classifier on that data

6. Go to 4 and repeat

This captures the notion of a model being trained on the data it outputs. The high level picture of the behaviour is fairly simple: there is some error incurred, dependent on N and D. That error is how far you'll be off after making a new model. Each time you do a step, you continue to do a random walk with step size sampled from that distribution.

X axis is steps, Y axis is angle between true classifier and current classifier, in radians (0 is same vector, PI is completely flipped)

That picture was with N=1000 points at each step. If you only have N=10 points at each step, your error is larger so your step size is much higher.

Instead of throwing out the data after each step, if you continue adding it to a dataset that grows larger at each step, it's a random walk with decaying step size (this used N=10 because N=1000's dataset gets too large to run 10000 steps)

Those results were in 2D. As dimension D gets larger, your error is larger and you'll need a larger N.

X axis is N, Y axis is difference in angle after 1 step, plotting the mean of 1000 different random initializations

When you try and study this analytically, you end up with some really messy equations in terms of this thing. Here's my messy code for much of the feedback analysis, ctrl-f for "convert cdf to pdf by differentiate" to find the symbolic solution. I didn't find this analysis much more insightful than just graphing it, since it's so messy.

Discrete Generative Models

The simplest setting is probably polya urn models, which are heavily studied.

However I think n-gram models are more relevant to the idea of "language models training on data produced by other language models", so I'm going to be studying those.

There's a few non-trivial decisions one has to make here that can matter for what your outcome is:

How do you generate the data?

I'm assuming that the model is originally given data that looks like this

<START> a a b a <END>

<START> a b a c <END>

<START> a b c d <END>

etc.

For bigrams I do this. In general, for n-grams, I have (n-1) <START> tokens. I think it's more useful to think about "context length" instead of n-gram, where a bigram model has context length 1. Then I can just say that there are contextLength <START> tokens.

I have the <START> and <END> tokens because this is realistic to how language models are fed data in the real world, and also because it lets me avoid questions about where to start generation.

However, now when I'm generating data from the model, you have an issue of not being able to control how long the outputs are. There are a couple different options:

- Truncate the generated data at some fixed length.

There are two decisions to make here:

- What happens if you get an <END> token before you reach that length?

APPEND: You could start generating a new sequence (starting with <START> tokens) and append it to your sequence.

END_EARLY: You could just allow the generated sequence to be shorter. To keep roughly the same amount of data at each step you can just generate sequences until the number of total characters you have generated is roughly what you wanted.

If you think about it, these two solutions are basically the same. With END_EARLY, we are generating stuff until we have about as many characters as we want. With APPEND, we are generating stuff until we have as many samples as we wanted, each of some length (so, as many characters as we wanted). From the models' perspective, both settings seem the same due to the <START> tokens not letting you see content from the previous sample. However, APPEND ends up needing to truncate more (see the bullet point below), so I prefer END_EARLY.

- What happens if you never get an <END> token but you have reached your target length?

If you append the <END> token after truncation, this is not a good idea because it'll add edges to <END> that didn't exist in the original graph, so the analysis gets much more messy and I think it's less reflective of reality. Bot comments might be cut off at the end of a sentence, but that's a plausible <END> boundary. It seems unlikely they would be often cut off in the middle of a word, for example.

If you don't append the <END> token after truncation, your learned model at the next step can end up with "sinks" that don't end in the <END> token. This happens if the only time it generated a string like "a b b" in a dataset is at the end of a truncated sequence. This isn't technically a problem, but it makes the analysis more messy when all these sinks start popping up, so it's better to avoid them.

You could just reject the sequence and generate a new one. This seems like the best solution to me. Just make sure that the "rejection size" is large enough that you don't significantly bias the sampling. This is another good reason for using END_EARLY.

So in summary:

- Start with a contextSize <START> tokens, and generate text until we reach an <END> token

- If the generated sequence is longer than some maxSize (maxSize is roughly size of largest input of originalDataset*10 so the vast majority of sampled things aren't rejected), throw it out.

- Keep generating sequences until number of tokens generated is >= dataSize

This will have some variance in length per run, but for large enough dataSize this should be negligible.

Using this strategy, we can say a few things:

- For any contextSize, after training our first model we can consider the graph where each node is a context (x_1, x_2, ..., x_contextSize) and each edge (x_1, x_2, ..., x_contextSize) -> (x_2, x_3, ..., x_contextSize, x_next) is the transition probability of generating x_next given that context. Thus, the behavior doesn't actually change for larger n-gram, the size of the graph just grows. Just looking at the graph structure itself (which is all that matters), WLOG we can consider bigram models. Any higher grams just restrict the graph so edges can't exist unless the context overlaps, and this constraint doesn't apply to bigrams. Of course, when considering how far we have diverged from the "original data distribution" we need to consider what our contextSize is.

- The probability of every edge in our n-gram graph goes on a random walk, up or down. The step size is smaller the more that edge is represented in the data. For every node that has multiple edges going out of it, eventually one edge will walk to probability 1.0 and the others will walk to zero. 

- We can say a little more than that. Every path from <START> to <END> that doesn't visit any nodes more than once has a non-zero probability of becoming the "converged path" that our random walk eventually converges to. Every other edge will be zero, and that converged path will have probability one. Thus, we will converge to determinism at the limit, and prune away everything except that converged path.

- "Not visiting nodes more than once" is important because any "loopbacks" will eventually be pruned away, because there is some point in that loop where a branch happened, and all branches eventually get pruned to a single output edge path.

- The character following any node is only dependent on that node, so at the limit of data the behavior of the random walk is only dependent on that node, nothing upstream or downstream. However, simple paths have deterministic length, while cycles will have some variability in how frequently they show up. This means that the step size can vary (for example, cycles might be overrepresented in the dataset, and thus their step size will be smaller), but I'm still figuring out the precise details of this.

I ran some experiments and verified that this is actually what happens for simple n-gram models. This isn't surprising and wasn't technically necessary, but I think it's good to check. I started with a word-level bigram model shakespeare and after 10000 steps it converged to "Please you see then?" and "By being miss\'d, I will not wish thee apart Cousin of duty,".

General Analysis Insights

For simple machine learning models, the distribution of the margin sorta represents the distribution your step size is sampling from (depending on how the decision boundary is determined from the data). This can be difficult to calculate, even for something simple like linear regression. Even the coin's distribution of step size can be pretty tricky, it's this bumpy thing. Zero at pr 0, zero at pr 1, and sorta this bumpy parabola that goes up and then back down in inbetween.

With the coin setting, you can say something simple like "a biased coin with heads of probability p will eventually converge to all heads with probability p and all tails with probability (1-p)". This is essentially via induction over the steps. Temperature affects this by making less than 0.5 more likely to converge to H and more than 0.5 more likely to converge to T, but I'm not sure yet exactly how.

You can also abstract to just talk about a random walk, and then random walk results apply. These results give good insights on why having grounding can really help: by biasing your walk towards a certain point.

There are forces that pull towards model collapse. Temperature < 1.0 is one of those forces, as are "loopy data" ("hello how are you hello how are you"). 

There are forces that seem pretty neutral towards model collapse.

There are forces that prevent model collapse. It would make sense that increased diversity of outputs helps. Grounding (having some of the data be true data) is also helpful, as is filtering outputs to be "quality inputs" (say, using a reward model) before they go back into the model.

Preventing model collapse is about making sure that more things prevent model collapse than cause model collapse.

I'm still learning a lot of detailed ML statistics. I think there's a lot of analysis to be done in this setting, and I encourage anyone to do that if they are interested.

Language Modeling

The above analysis gives us some insights, but it would be good to test this on modern models. Language models are a natural choice. I'll be fine tuning GPT-2.

These can take a while, so I only had time to do the experiments without grounding. I'd still like to run more runs to be confident about the implications here, but here's what I have so far.

The x axis is steps (each step is generating a new dataset of 4000 tokens and doing one epoch of fine-tuning), the y-axis is entropy. I'm estimating entropy of the model by generating 200 sentences. For each sentence, I sum the log probs of each token, to get the probability of the entire sentence. Then I average over those 200 sentences to get the log prob of the model, and negate the value to get entropy.

Most of the runs I stopped early because it was clear they basically stuck. However those in the middle it was still unclear, so I ran them for a little longer:

I'm hesitant to say anything concrete about these without running more runs, because I don't have enough data to draw solid conclusions. However, the general gist seems to be this:

Runs either collapse to repeating the same thing over and over, or go to entropy. There is some probability of doing either of those things.

When temperature isn't too strong, they initially spend some time "getting used" to how weird many of the language model outputs are. Once they've done that, they'll encounter loops like "I have a cat I have a cat I have a cat". If those loops are outputted in the dataset, they'll be more likely to be outputted in the future. Thus, the model focuses on those loops

Temperature of 1.0 tends to eventually decay. Things above 1.0 have some probability of shooting off to noise (very high entropy) and getting stuck there. The higher the temperature, the more likely this is to happen.

Things below 1.0 tend to decay to "repeating the same thing over and over" pretty quickly.

Future work

I'd love to see more detailed analysis about the effects of temperature on language model bias (in the fairness sense) after a single step of fine tuning. It seems like you could do some kind of n-gram analysis of the outputted tokens to suggest that there are biases, for example.

It also might be possible to fix the temperature issue, by tweaking the model loss to account for the temperature (Instead of asking for pr 1.0 of the target token, as for pr temperature(T, 1.0) of the target token). I don't think this will quite do the right thing, but it might help, it would be interesting to see if something like this is helpful.

The other direction this kind of work can go is fixing the limitations of this model. Consider the setting of "Language models output text into the world, and that text is fed back into models". This framework I've discussed above is missing two important bits:

- Grounding: Some of the data at each step is not from models, it's from some baseline "true distribution", such as humans. 

In this setting, this acts as a bias to the random walk, always pulling it towards the true place. It's sort of the opposite of temperature in this way. Just a very small bias can make a big difference: in the linear classifier setting 1/100 of the data being from the true distribution was enough to prevent the random walk from drifting too far away. However, it would be interesting to study how grounding affects the behaviour of language models. It seems like the effects of temperature can be very strong, so you may need quite a bit of grounding to counteract those effects. Also, the higher dimensional your data is, the easier it is to walk in a bad direction, so you'll need more grounding.

Note that in reality, the model distribution and the true distribution influence each other. You could try and model this as multiple models, each influencing and seeing data from each other. Once you do this, in simple coin settings you can essentially just look at the "center of mass" of the models (it's a little more nuanced because you need to do the center of mass relative to a single model's weighting, but center of mass is the intuitive idea). That center of mass will take a random walk, and the above analysis about collapse applies.

So without any "hard grounding", how are humans avoiding collapse? After all, we are all outputting data and then processing that data to update our internal models in some abstract sense. I think the answer is:

- Feedback/Selection: Some of the model outputs are ignored, and not sent back into the model. For example, the model outputs might be bad and not put back on the internet.

This feedback process is more general. With GANs, the generated samples that are able to fool the discriminator are used for later training. With AlphaGo, only the winning moves are fed back into the model. With reward modeling, we are feeding back in the good outputs, and not the bad outputs.

These systems have worked well in practice, which suggests that this feedback pressure is sufficient to overcome the tendency towards collapse.

I plan on moving on to other things, but anyone should feel free to push these results further if you're interested.

Speculative section:

It seems like there's something even more general happening here, related to play. I will loosely define play as:

- Look for new tasks where you can measure how well you are doing

- For the tasks where you can make some progress, optimize their metrics until you can improve more doing something else

Essentially you are exploring, making up new games where you can actually make progress, and then making progress on those.

Most of the "self-play" settings we have are set up in a way where there's this implicit curriculum, so "just get better than the opponent" is a task where you can make progress. Essentially, it makes "finding new tasks" fairly easy. But I think ideally you want more emphasis on the exploration of possible tasks. This is sort of a research direction, on "learned sub-tasks". But I wonder if you can make it more "playful", where there isn't an end goal aside from "progress on tasks I came up with". Intrinsic motivation literature suggests that agents have some preference over choosing some tasks than others, and I'd like to understand some of those mechanisms as they probably point to the kinds of advanced exploration of tasks intelligent agents need to be doing. Artificial creativity and quality diversity research suggests that open-ended exploration is important for eventually finding good solutions to problems you care about, so this seems like an important direction to investigate more. It also seems like the core piece in a lot of what makes open-ended culture and opinion formation work. It'll probably be the direction that I'm investigating next, how to get agents to "play" in some open-ended sense, in simple musical or predictive text settings.