Encoding cellular automata into gradient descent

After downscoping my project to just "training a model on its own outputs", I've been writing up a first draft on Overleaf. I found it more difficult initially than writing a blog because I felt like it was "supposed to be good", wheras in a blog I don't really care who reads this so I can just write out my thoughts like I'm explaining them to someone. Eventually I learned that that concern over your writing being good makes it hard to write, and it's better to just have a bad rough draft and then polish it into what you want. I have to keep reminding myself of this, but it does make the writing workable.

However honestly I feel like I downscoped my project a little too much? I have a detailed analysis written up I'll eventually post of why this is the downscoping I did, and unfortunately I feel like further research in this direction would take more time than I have. But I feel like my writeup won't take the month more that I have remaining, so I wanted a small project I can work on when I get stuck in writing and need to think through things more.

My previous project was ultimately about trying to have formal theories to predict the learning trajectories of neural networks. I've still been thinking about that for a while, and realized a bit ago that there might be a fairly simple way of showing a hardness result:

Encode Rule 110 into a neural network, so a set of parameters encodes the state, and one step of gradient descent uses Rule 110's transition function to update those parameters into the next state. For example, imagine that at t=1, the second layer of biases are 010110. After doing gradient descent for one step, the second layer of biases would be 111110. After doing it for another step, they'd be 100011, then 100110, and so on. Which parameters to encode the states in matter, and I'm assuming a fixed input and output (because this should be very easy to do if you carefully setup the inputs and outputs).

Rule 110 is a simple cellular automata that can encode turing machines, so this would show that any theory that claimed to prove things about long term learning trajectories in general would need to solve the halting problem. This theoretical result may not apply in practice, but it would nicely articulate why the problem is so hard.

I had poked at this a while ago, but got stuck because the math got messy. However I realized that that's a good use for sympy, so I've spent some time encoding the dynamics of gradient descent into sympy, a computer algebra system.

After getting that working (and checking it against pytorch), I did the following, for a fixed network with all layers of size N (initially 3 deep):

- For every possible binary string of size N, create a new set of bias and weight variables

- For each set of bias and weight variables, set first hidden layer's biases to the state.

- Apply rule 110 to the state to get what the state should be next. Also apply gradient descent (symbolically), to see what the actual parameters would be after one step. This lets me create an equality constraint for every parameter, because they need to equal the parameters of the next state

Doing this, I've learned:

- For a network of any depth and width, with a X^2 activation (chosen to make it possible to solve), MSE error, and a fixed input and target, it's impossible to encode rule 110 into the biases of any layer

This is definitely true for the encoding it into the first layer's biases. It's true for the later layer's biases, as long as the tree of states going into the 0* (all zeros) state is actually a tree (this seems to be the case so far for all the sizes I've looked at, but I haven't proven it yet)

Essentially this result works because the 0* state maps to itself, and this creates constraints that force the input to be zero (knowing this, you can also set the weights of the input->first hidden layer to zero, because they don't matter anymore, but that'll happen anyway by default if you just recompute the constraints)

Once you do that, for encoding 110 into the first layer of biases, this immediately gives you the constraint 1=0 which is unsatisfiable.

If instead you are encoding 110 into the second layer of biases, this forces the biases of the first layer to also be zero, but only for the 0* state. That effect trickles up into the tree thing that always seems to exist and feeds into the 0* state, and eventually once it reaches a leaf you get a contradiction and a 1=0 constraint.

If you are encoding 110 into later layers of biases, you can follow the above process to successively show that layers need to output zero until you read the layer before your layer, which then gives you a 1=0 constraint.

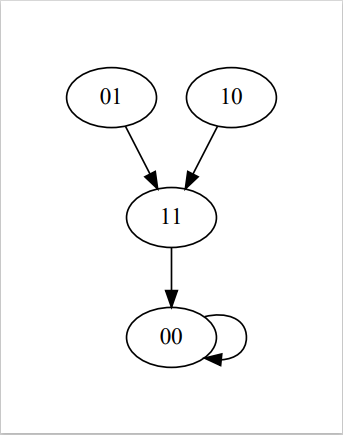
For example, here are some graphs for different numbers of bits:

As you can see, there always seems to be that 0* tree piece. Sometimes there is other stuff, but that 0* bit seems to be sufficient to make a contradiction. 

This is not a formal writeup, I'll still playing with the maths to see if there's something that could work. While answers of the form "this specific version of the proof technique don't work" are useful to share, I'd still like to see if something could actually work first. I could also try encoding things into the weights: maybe there's a way of "reading out" the states of 110 in a polynomial time way (in terms of the size of the state) from a weight matrix, which would still be sufficient to show the negative example. Alternatively, we might be able to still make the impossibility result if we simply constrain the states to not being within the 0* tree piece of the graph. 

To be fair, this isn't exactly an impossibility result. Turing machines require an infinite tape size, and if we constrain the number of states (and loop at the boundaries) then 110 is just a finite state machine. However, the number of possible states is exponential in terms of state size, so it's still computationally difficult. If I end up getting 110 encoded into gradient descent then I'll elaborate further on these nuances.

If it turns out it's possible to encode 110 into a graph, this actually does give us more than just an impossibility result. It's another lens at looking at gradient descent itself. The long term goal of a project like this would be to phrase gradient descent as linear combinations of automata, then you could use theory to sometimes predict what's happening. It wouldn't work in general, but as the saying goes "a hardness result is the first step to solving a problem".